引言 本文中主题是内生性,它可能严重偏向回归估计。我将专门模拟由遗漏变量引起的内生性。在本系列的后续文章中,我将模拟其他规范问题,如异方差性,多重共线性和对撞机偏差。
数据生成过程
考虑一些结果变量的数据生成过程(DGP)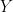
 :
:




对于该模拟,我设置参数值
 ,
,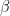
 以及
以及
 与模拟正相关的独立变量,
与模拟正相关的独立变量,
 和
和
 (N = 500)。
(N = 500)。
| 1 2 3 4 五 6 7 8 9 | # simulation parameters
set.seed(144);
a=50; b=.5; c=.01; x=rnorm(n=ss,mean=1000,sd=50);
z=d+h*x+rnorm(ss,0,10)
|
模拟
模拟将估计下面的两个模型。第一个模型是正确的,它包含实际DGP中的所有术语。但是,第二个模型省略了DGP中存在的变量。相反,变量被误入了误差项 
 。
。




第二个模型将产生一个有偏差的估计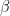
 。差异也会有偏差。这是因为它
。差异也会有偏差。这是因为它
 是内生的,这是一种说它与错误术语相关的奇特方式
是内生的,这是一种说它与错误术语相关的奇特方式
 。由于
。由于
 和
和
 ,然后
,然后
 。为了说明这一点,我在下面进行了5000次迭代的模拟。对于每次迭代,我
。为了说明这一点,我在下面进行了5000次迭代的模拟。对于每次迭代,我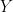
 使用DGP 构造结果变量。然后我运行回归估计
使用DGP 构造结果变量。然后我运行回归估计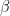
 ,首先是模型1,然后是模型2。
,首先是模型1,然后是模型2。
| 1 2 3 4 五 6 7 8 9 10 11 12 | sim=function(endog){
e=rnorm(n=ss,mean=0,sd=10)
# Select data generation process
if(endog==TRUE){ fit lm(y~x) }else{ fit=lm(y~x+z)}
return(fit$coefficients)
}
sim_results_endog=t(replicate(trials,sim(endog=TRUE)))
|
仿真结果该仿真产生两种不同的采样分布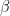
 。请注意,我已将true值设置为
。请注意,我已将true值设置为
 。如果
。如果
 不省略,则模拟产生绿色采样分布,以真实值为中心。所有模拟的平均值为0.4998。当
不省略,则模拟产生绿色采样分布,以真实值为中心。所有模拟的平均值为0.4998。当
 被省略,仿真得到的红色采样分布,围绕0.5895居中。它偏离.5895的真实值。此外,偏差采样分布的方差远小于周围的真实方差
被省略,仿真得到的红色采样分布,围绕0.5895居中。它偏离.5895的真实值。此外,偏差采样分布的方差远小于周围的真实方差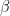
 。这会影响对真实参数执行任何有意义推断的能力。
。这会影响对真实参数执行任何有意义推断的能力。


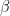
 可以通过分析得出。考虑在模型1中(如上所述),
可以通过分析得出。考虑在模型1中(如上所述),
 并
并 
 通过以下方式相关:
通过以下方式相关:



 用等式3 代入等式1并重新排序:
用等式3 代入等式1并重新排序:




省略变量时
 ,实际上是估计的等式4。可以看出,
,实际上是估计的等式4。可以看出,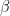
 数量有偏差
数量有偏差
 。在这种情况下,由于
。在这种情况下,由于
 并且
并且
 通过构造正相关并且它们的斜率系数是正的,所以偏差将是正的。根据模拟的参数,应该是“真实的”偏差
通过构造正相关并且它们的斜率系数是正的,所以偏差将是正的。根据模拟的参数,应该是“真实的”偏差 
 。这是偏差的分布,它以.0895为中心,非常接近真实的偏差值。
。这是偏差的分布,它以.0895为中心,非常接近真实的偏差值。


上述推导还可以让我们确定从知道的相关偏差的方向
 和
和
 以及的符号
以及的符号
 (的真局部效果
(的真局部效果
 上
上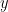
 )。如果两者都是相同的符号,那么估计值
)。如果两者都是相同的符号,那么估计值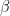
 会有偏见。如果符号不同,则估计值
会有偏见。如果符号不同,则估计值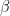
 将向下偏移。结论上面的案例很一般,但有特殊的应用。例如,如果我们认为个人的收入是教育年限和工作年经验的函数,那么省略一个变量将偏向另一个变量的斜率估计。
将向下偏移。结论上面的案例很一般,但有特殊的应用。例如,如果我们认为个人的收入是教育年限和工作年经验的函数,那么省略一个变量将偏向另一个变量的斜率估计。
还有问题吗?联系我们!
-中国专业的第三方数据服务提供商,提供定制化的一站式数据挖掘和统计分析咨询服务
统计分析和数据挖掘咨询服务:(咨询服务请联系)
 QQ:3025393450
QQ:3025393450


【服务场景】
科研项目; 公司项目外包;线上线下一对一培训;数据采集;学术研究;报告撰写;市场调查。
【大数据部落】提供定制化的一站式数据挖掘和统计分析咨询服务



